Carnival of Mathematics 224

Roll up, roll up, roll up. Come hither come all to the Carnival of Mathematics. This is the 224^th Edition of the longest running Maths Carnival.

For those of you who are unaware, a “blog carnival” is a periodic post that travels from blog to blog and has a collection of posts on a certain topic. In this case the topic is mathematics.

224 is an interesting number – you can make some simple number sentences out of it for a start 2 + 2 = 4 and 2 x 2 = 4, even 2 ^ 2 = 4, if you’re feeling a little spicy! It is an abundant number, and admirable number and is also the perimeter of a Pythagorean triple! (which one you say? I’ll leave that as an exercise for the reader……) For more fun facts about the number 224, try this post here!

It has been a long time since I have had the honour of hosting the carnival, in fact it was the the 126th edition I last hosted (available here). Lots has gone on in the world of mathematics since then, and the most recent carvinval, edition 223, is available here, hosted by the great George Shakan at his Data Science and Math blog.

This month we’ve had some quirky submissions, and none quite as quirky as the first one I recieved, submitted by Katie, that is the “Minimum Wage Clock“, this is not for the faint hearted, as it shows in real time the vast difference in earning between those on minimum wage, and those in high up positions.

Sticking with the quirky theme, next up we have another submission from Katie which looks at some excellent research and data collected by an eight year old girl, who really is a data scientist in the making.

If you, like me, get annoyed at various words and semantics, then this thread on mastadon may have you giggling, or up in arms!

For those of you, like me, who are secondary maths teacher, this post from Jo Morgan at Resourceaholic has some highlights to help you get your classes ready for this summers GCSE exams.

While Dave Gale, at reflective maths, has these fun questions based around the no 2024.

If it’s maths news you are after, then Katie Steckles and Peter Rowlett over at The Aperiodical (the custodians of this very carnival) have got you covered with this excellent news round up.

If you’ve after something lighter, the wonderful Ben Orlin has put out a few of his hilarious post this month at Math with Bad Drawings, always worth checking out.

Prof Nira Chamberlain, president of the mathematical association, has Dr Jeffery Quay as a guest on the latest on his excellent VLog series “What’s the point of maths?”

Well that’s it for this months carnival – I hope you enjoyed it! While you’re here, you could check out other carnivals you may have missed at the Carnival’s homepage.

Sine and Cosine – do we need a formula?

While teaching non-right angled trig recently it occurred to me that when doing the questions myself, I don’t actually thing about the formula all that much. Particularly with the sine rule. Yet I still start the teaching of it using the formula heavily. It made me wonder if this was really all that necessary.

Firstly the sine rule. Here in this question I have two “opposite pairs”:

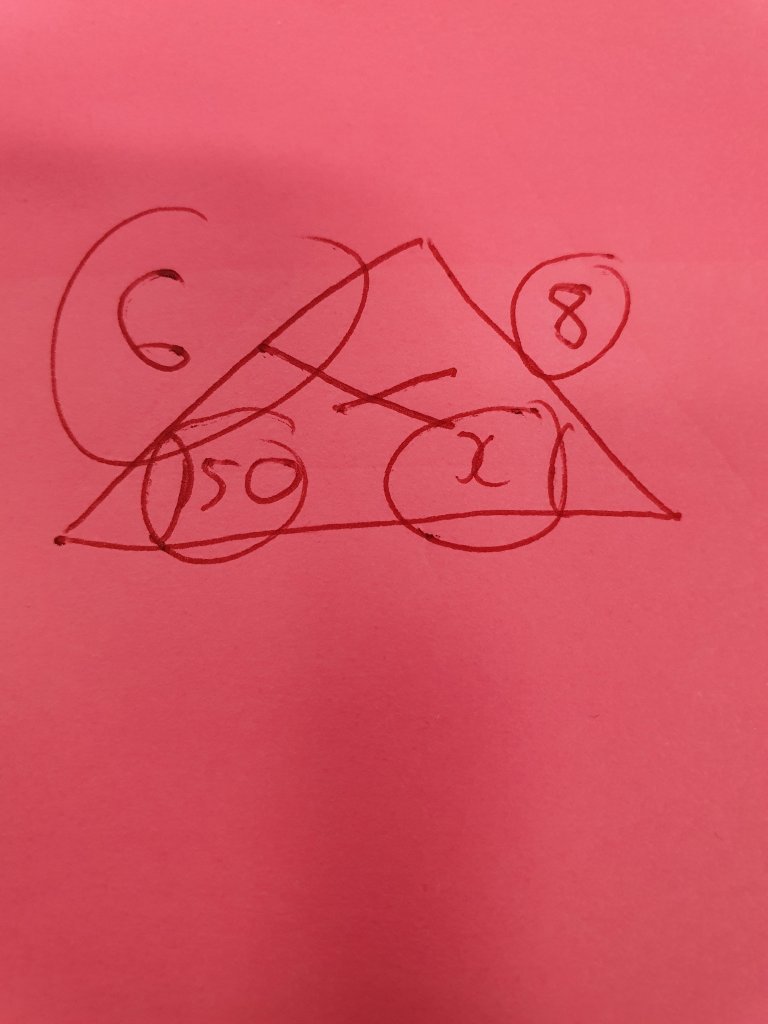
And I know that the ratios of side:sine of angle for these opposite pairs are the same, so I can easily set up an equation and solve. Not once in that process have I thought about or used the sine rule as it comes, in terms of a,b and c. The triangle isn’t even labelled, but I can solve the problem. I can also talk about ambiguous cases as and when they crop up.

The cosine rule on the other hand requires a bit more remembering, and the formulae certainly comes in handy as memory aid (as does the sine rule) but sometimes students can become a little over focussed on the labelling. When I approach a question I don’t label the sides, I look for he pair – the side and opposite angle – and I know these both have to be in the place of a in the formulae.

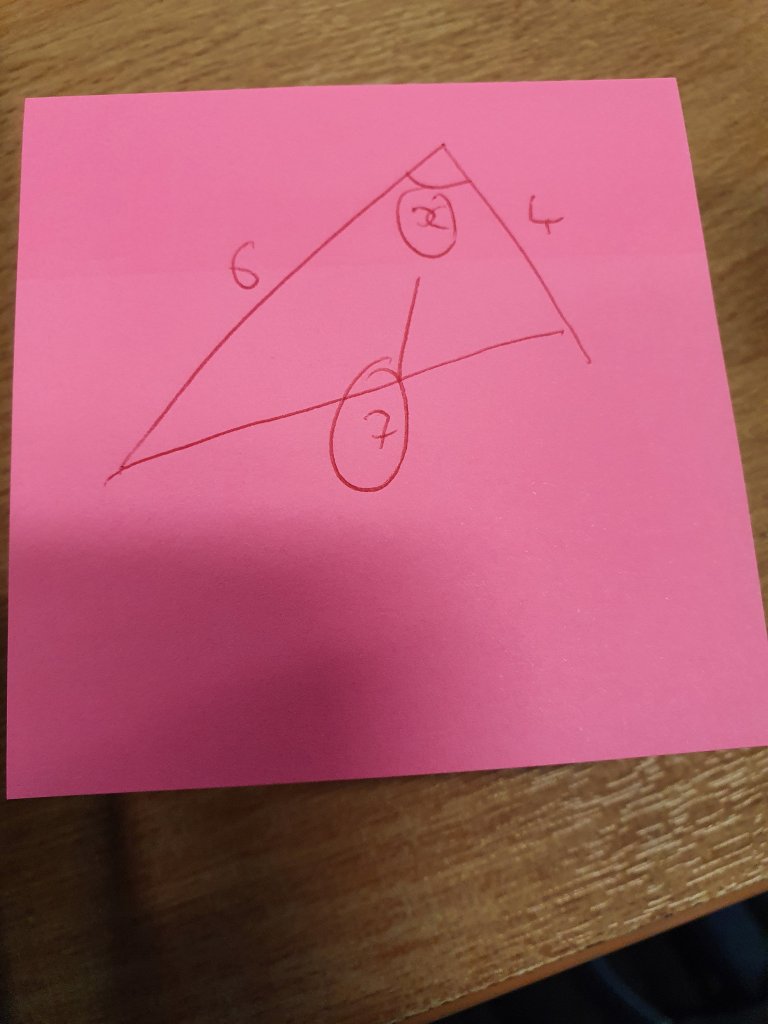
It makes me wonder whether there’s a better way to approach this. Certainly I find students get to grips with it quicker if I spend less time on labels and more time on pairs, know that the pair is a no matter what the labels say. I’d be interested in others thoughts.

Degree Level Apprenticeships for Teachers

Recently I’ve noticed a bit of discourse around the idea of Degree Level Apprenticeships as a possible new route into teaching. I’ve seen some good discussion around this and I’m currently sitting with a fairly open mind as to how it might go. I’ve seen people express concerns that there will not be a way to ensure that subject knowledge is adequately addressed. There are concerns that the government will be looking at it as a cost saving measure to drive down wages. There is plenty to worry about, to be honest. But I don’t know if it’s worth worrying too much yet. We have a recruitment and retention crisis in teaching, and we need to be exploring options that may alleviate this. Maybe Apprenticeships can help. But how would they work?

We already have a type of teacher training that is an apprenticeship. The post graduate teaching apprenticeship (similar to the old schools direct salaried route). This is a similar route as teach first I believe, in that trainees basically take their classes on their own from day one. I don’t think that this is a workable option. I think about all the year 13s I’ve taught over the years, and the throughout of them walking into a class and leading it from the get go a few weeks after their a levels is an idea that would terrify me.

I had a look at some course programmes for some current degree apprenticeships, they seemed to suggest that students would receive 20% of the time they were at work as study time, plus that they would have roughly 24 days per year in university. Applying this to a 25 hour timetable, I guess we are talking about 5 hours blocked off for university study, this could be a mixture of assignments and potentially some online content. This could be used for building subject knowledge and for pedagogical knowledge. Then the university days could cover both. Which would leave the 20 periods a week for the “working” part of it.

This is the part I’m really interested in, presumably the first year each class would have a host teacher attached to it – meaning that in order for it to be cost affective for the school the wage of the apprentice would need to be less than the money the school receives for the apprentice. The other alternative is a real throwing them in at the deepend situation of giving them classes and hoping for the best day one.

Perhaps the idea is to start them on one class in year 1, closely watched by a mentor, then in years 2 and 3 to expand the amount of students they have, and start to have times timetabled when it is just them and the class. I don’t know. Will be interesting to see.

I’d also like to find the retention rate for other jobs who have taken the degree apprenticeships route. The retention rate for teachers at the moment is around 59% (for ten years), apprenticeships have around the percentage actually make it to the end of their apprenticeship. So I’m not even sure it will help this.

If you have an opinion on this, I’d love to hear it either here in the comments or over on the socials. Also, if you have managed to find any more out than i have, please drop me a line too.

Triangles, Trig and Squares, oh my.

Over the weekend I happened accross this loevely puzzle on twitter. It was tweeted out by Diego Rattaggi (@diegorattaggi) and I saved it to my ever growing folder of puzzles to try on my phone. When i had a bit of time spare I thought I would give it a go.

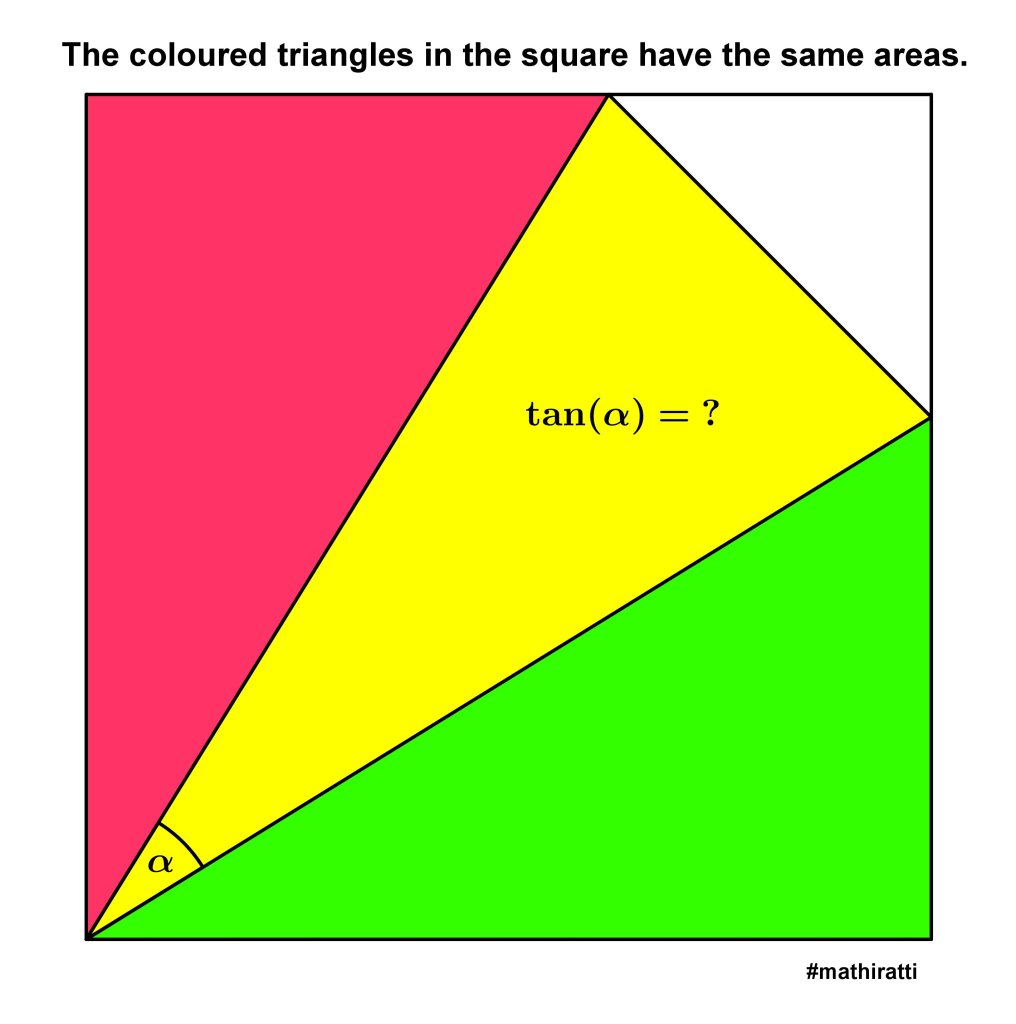
Have you had a try? If not, you should. Its a nice one and I’d love to hear some different approaches.

Anyway, here is how I approached it. Initially, I wondered about finding an algebraic expression that might fall out with some nice numbers, but i got a nasty looking equation with z and y both raised to the power 4 so I thought I’d try a different tactic.

I did plenty of annotating on a diagram to visualise the information, and found that 180 = 180, so that wasn’t particularly useful.

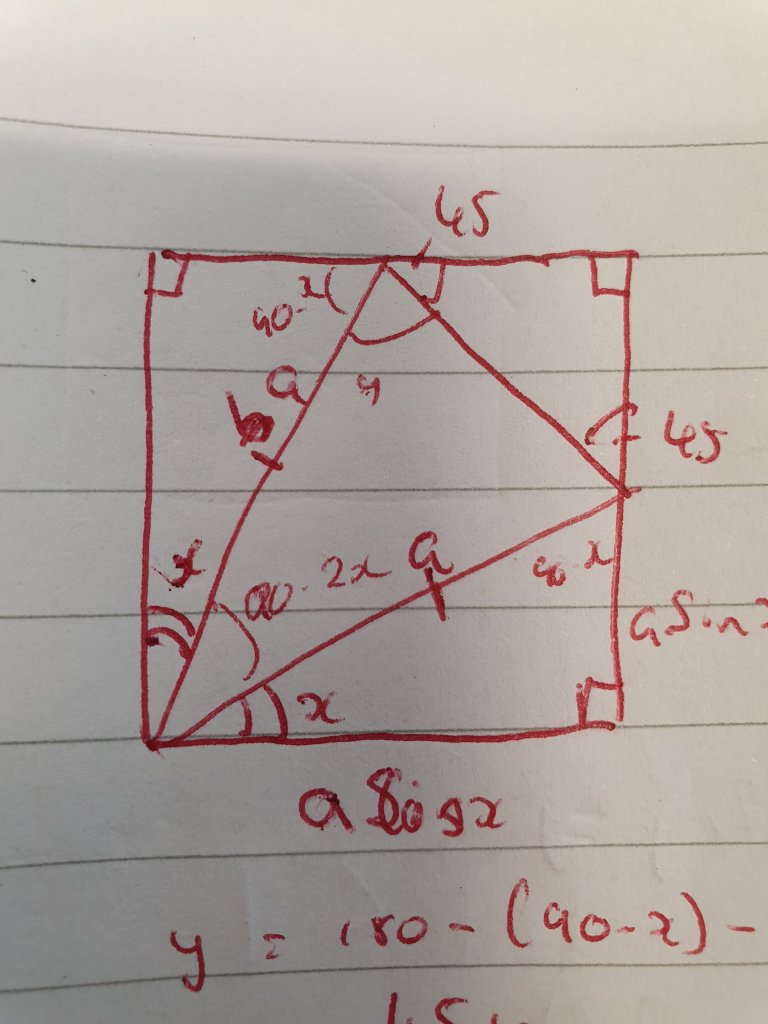
Then I looked at a trigonometric approach. Which fell out nicely.

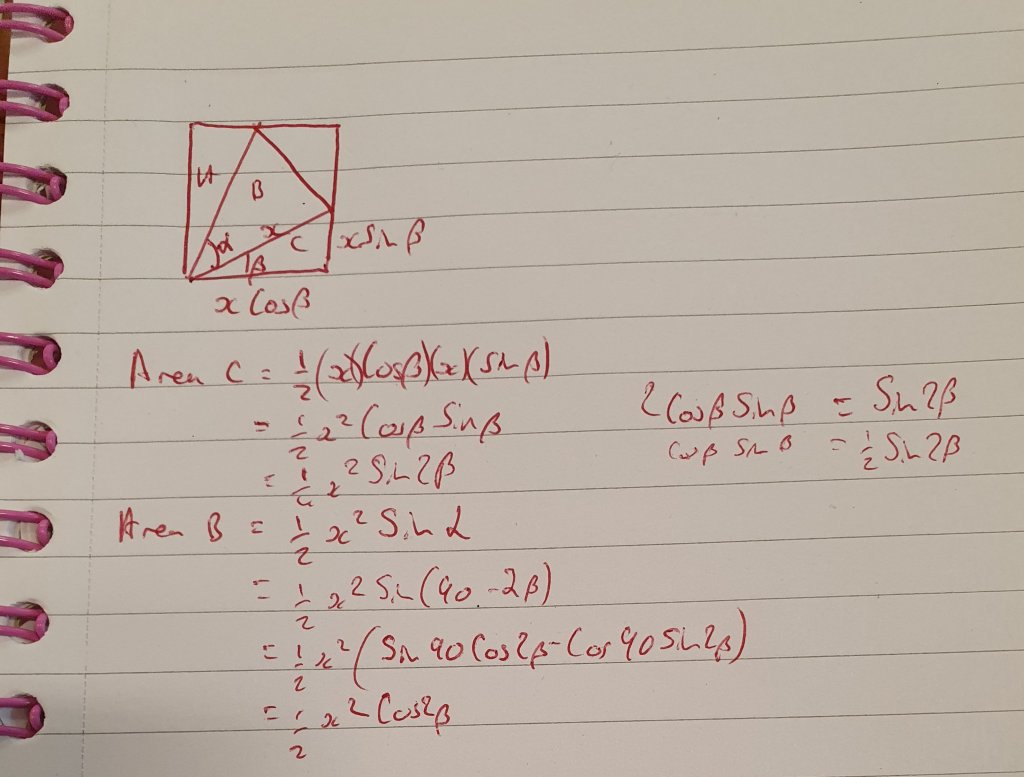
I has Tan 2b = 2, and I needed tan (90-2b), my insitinc was to use double angle formulae, but I quickly realised tan 90 was undefined so that wouldn’t work. I sketched a quick right angle triange, then realised I was being a tad silly.

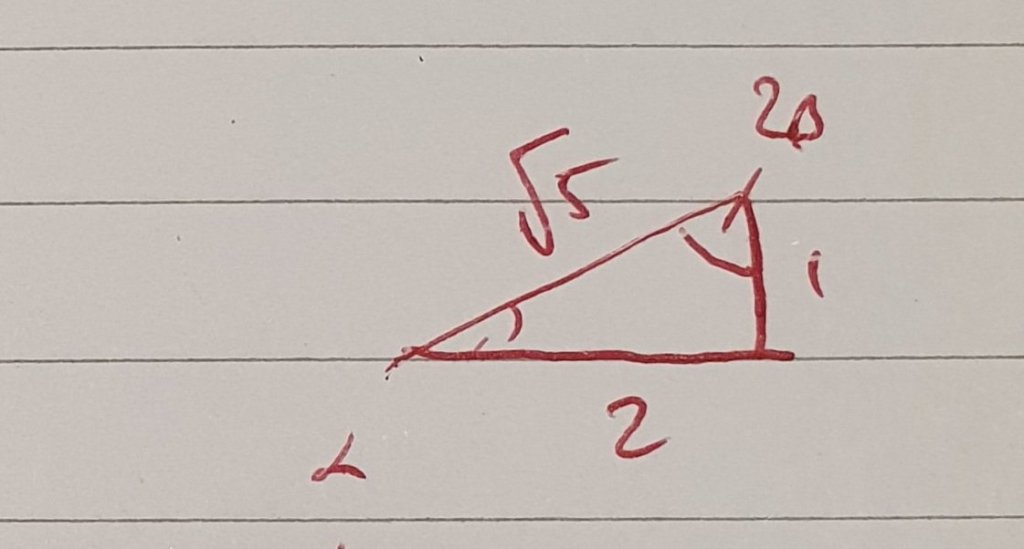
While the triangle did give me the correct answer, it also made me remember that the definition of Cotangent is “The tangent of the complementary angle”, so cot 2b is quite literally tan (90-2b), so all i needed to do was take the reciprocal.

It was a nice little puzzle that incorporated a number of things, and it has me wondering how my year 13s would approach it. I’m gonna try it out with them later this week. I’d be intrested to hear how you approaced it, expecially if you soved it a different way.

Revision, past papers and clarity of instruction

Recently I gave some of my year 12 students some practice papers as homework to aid their revision. When they brought them back in one of them had literally copied to  entire markscheme into to the answer paper, while another had watched a walk through and written up the answers with notes on how to do it next to each line of working. When I discussed with the class that there was absolutely no point in blindly copying the markscheme and handing it in as a) I already know the markscheme has the correct answers, and b) this isn’t getting them thinking about the maths and it really isn’t going to help them improve, they were all keen to point out that the other student had used a youtube walkthough.

 

This led to an interesting discussion with them. At first they couldn’t see a difference. I explained that actually, watching a walkthough and making notes on each line of working about what you are doing and why is actually a great way of revising. It is basically the same as me doing a walking talking mock with them. It allows them to see how a more experienced mathematician would tackle the questions and allows them to build their own thought process. So when a past paper is given to aid revision purposes, this is actually a decent use of it.

 

This led me to thinking about the instructions I had set. Those that copied the markscheme seemed to think the point of the homework was for them to get as many correct answers on it as possible. But actually, the point of the homework was for them to get as many correct answers on their upcoming assessment as was possible. A key difference, given that they will be doing their assessment in exam conditions rather than at home with textbooks and the internet freely available.

 

Perhaps I should have been more explicit with my instructions, using papers and exam questions for a variety of uses over the course of the year perhaps causes confusion if there is not additional information. I usually use exam questins and exam style questions in class and for home work to assess how well they understand toopics as we go along, I also use exams for data collection points, and then there is the use for revision. I think I need to work on explaining what each one is for when I’ve set it.

 

I’ve given them another paper to use as practice this week, I just hope that the discussion has an effect and that they use this one to help them prepare for the exam better, rather than to be more proficient copiers!

A pythagorean problem

Came across another nice puzzle from Mr Gordon (@MrGordonMaths):

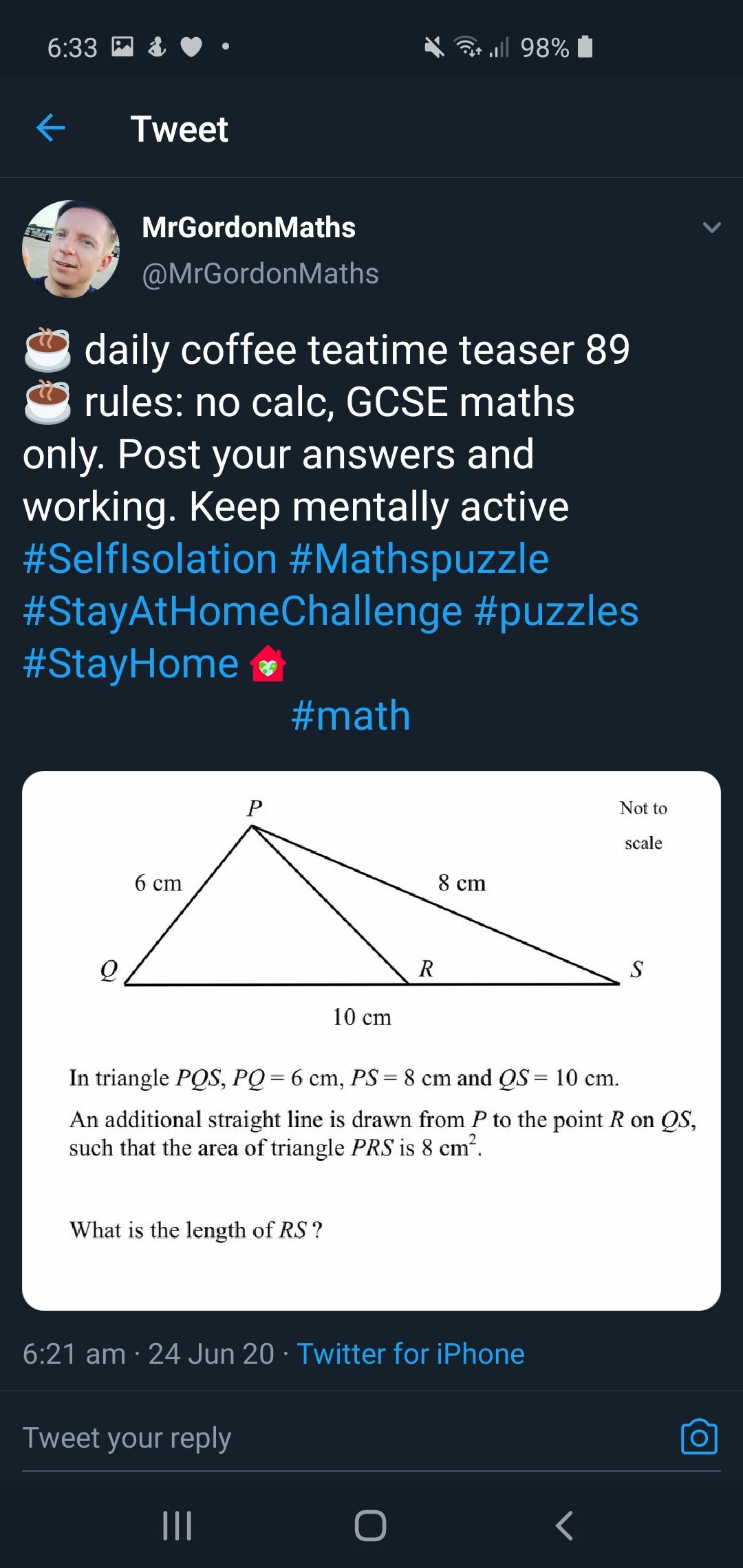
First thing I noticed was that it was a pythagorean triple. My initial thought was that there might be a solution involving circle theorems, but then I realised that as an area was given this might be the best route.

As angle QPS IS 90, then the area of triangle QPS is 24 (6×8/2). That means a perpendicular from P to QS must be 4.8 (as QS is 10 and would be the base on this instance.

The area PRS is given as 8 so the area of triangle QPR must be 16 (24 – 8).

This means that 4.8x/2 must be 16 (where x is the length QR. So x = 32/4.8 = 6 ⅔ so length RS is 3⅓.

At this point I realised that I’d actually gone a slightly longer than necessary way. As 4.8 is also the perp height of PRS when RS is the base I could have used that triangle. 4.8y/2 = 8 where y is length RS, so y = 16/4.8 = 3⅓.

I then realized QPR and PRS were both triangles with the same perpendicular height, and that as the area for each triangle is bh/2 then the ratios of their areas would be the same aa their bases. So as its 16:8 (or 2:1) all I really had to do was split 10 in the ratio 2:1 to get 6⅔:3⅓, and pick the smaller one as the length PR.

A lovely problem with a nice solution.

Accumulator maths

Earlier today I was discussing and thinking about football accumulators, and accumulators in general. In case you don’t know what one is here is a quick overview. You basically pick a set number of bets and put an initial stake on, then if your first bet wins the winnings and stake roll over to the next bet etc.

The idea behind them is quite interesting. The more bets within your accumulator, the more you can win and the growth can be exponential.

For instance, if you backed a number of football teams all at 2-1. If you put a quid on, and bet on the one match, you’d finish with 3 quid (£1 stake returned and £2 winnings). If it was 2 matches then that 3 quid would roll to the 2nd match and if they won to you’d end up with 9 quid. A third match and you’d have 27, a 4th and you’d have 81n a 5th 243, a 6th 729, 7th 2187 8 matches 6561 etc. Its a geometric series.

I thought about this and thought it might prove an interesting real live discussion on exponential growth and geometric series. You could see how quickly these things would grow. As most accumulators aren’t all the same odds you could discus how these models change with different amounts and this would lead to nice discussions around commutativity and the like.

I then wondered if this was something that should be discussed in a lessons. Gambling can become an addiction and it can ruin lives. It might have already affected the lives of students in our care, and discussion on it in lessons might be seen as promoting it.

I then started thinking about some of the topics we do teach, and the origins of it. Vast swathes of the maths we teach stems from mathematicians trying to get an advantage in some game of chance or other. And although we might not talk about the gambling we still teach the maths that came about from it.

The maths that comes from accumulators is very interesting, as is a lot of maths with roots in gambling. I would love to discuss it, but think it’s a topic to be wary of. I’d love to hear your views. Do you discuss this sort of thing in your lessons? Do you manage to do it in a way that doesn’t promote gambling? Do you think we should leave it out of lessons? Please let me know in the comments or via social media.

Envelope puzzle and neat little square

I’ve been looking through my saved puzzles again and I found this nice little one in the maths newsletter from Chris Smith (@aap03102):

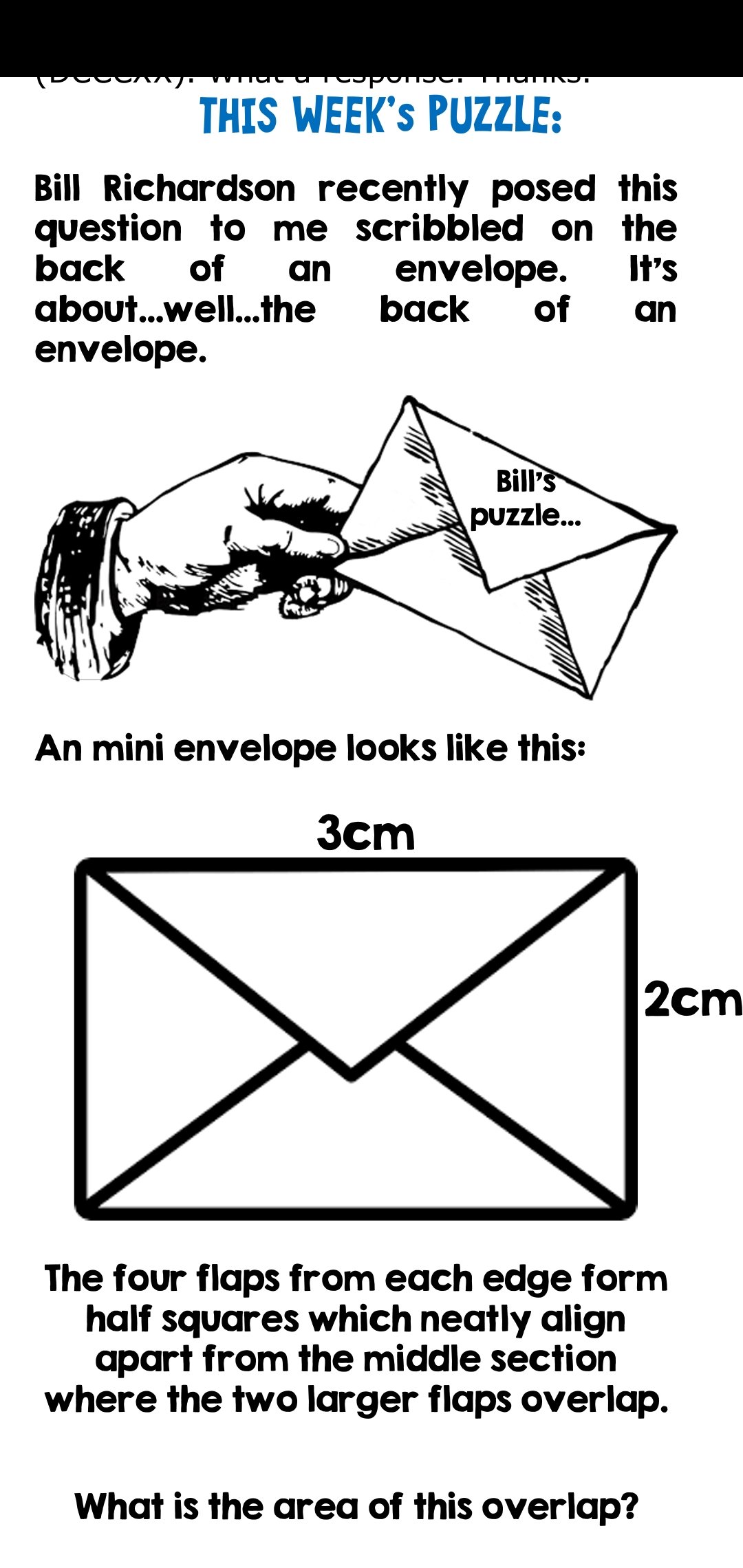
It’s a nice little question that took me some thinking about.

First I considered the half squares with hypotenuse 2. As these are isoceles RATs, that means their side length is rt2 so each has an area of 1.

Then I thought about the half square with hypotenuse 3. Again it’s an isoceles RAT so pythagoras’s theorem gives us a sidelength of 3/rt2. So an area of 9/4.

These 3 half squares add to 17/4. The area of the rectangle is 6 so the part not covered by the half squares must be 7/4.

When thinking about the overlap, we need to consider what that means. I assume it means the bit that goes over the others, so in this case 9/4 (area of the halfsquare) – 7/4 (area of the gal). Which is 1/2 cm².

I think this is an amazing little question that I cant wait to try out in class. It also got me thinking about the square with diagonal of 2 and area of 2. It’s an interesting square really, and the only one where we see this. Consider a square, side length, x. The diagonal is (2x²)^½, the area is x². If we equate the. And square both sides we have 2x² = x⁴ , or x⁴ – 2x² = 0, so x²(x² – 2) = 0. This generates a solution when x = 0 (which is trivial and discountable as no square can exist without side length. We also get positive and negative square roots if 2. But we can ignore the negative as lengths in this case are scalar, so we have one answer. It’s a neat little square.

1-9 math walk

Today I want to look at another puzzle I found on math walks (from Traci Jackson @traciteacher):

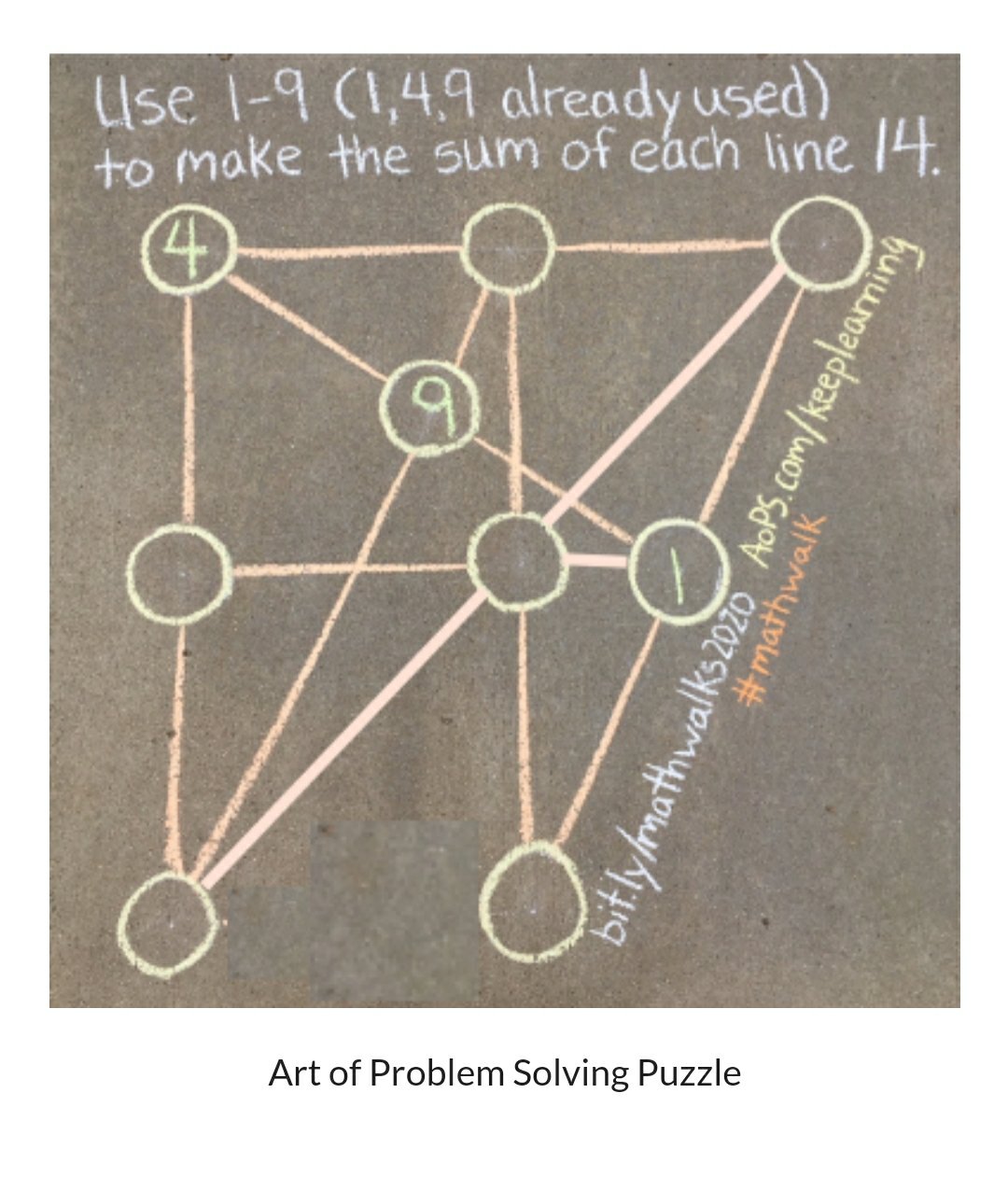
I love these 1-9 puzzles, and thought I’d have have a crack.

First I considered the 9, with the 1 gone already that means that the 9 must share a line with the 2 and the 3 to make 14.

That means that the 4 shares 1 line with a 2 and one with a 3. That means the 4 is one lines 4,2,8 and 4,3,7.

I considered these lines:

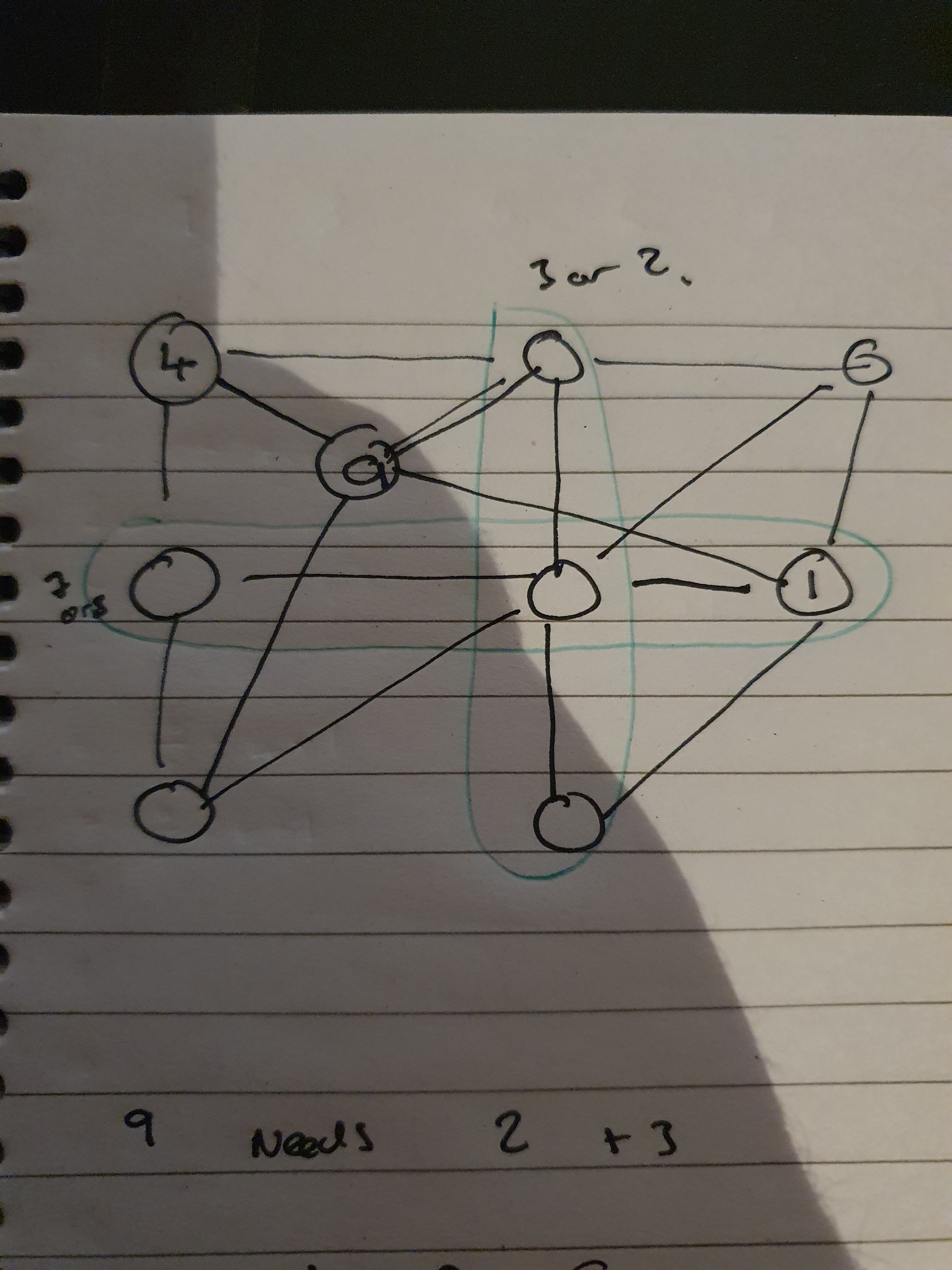
If I put the 7 on the left, I’d need the 6 at the intersection of the green lines. That would also mean that the 2 was above it, but I’d need another 6 on that line which doesn’t work.

So the 8 must be on the left and if we follow through we get:

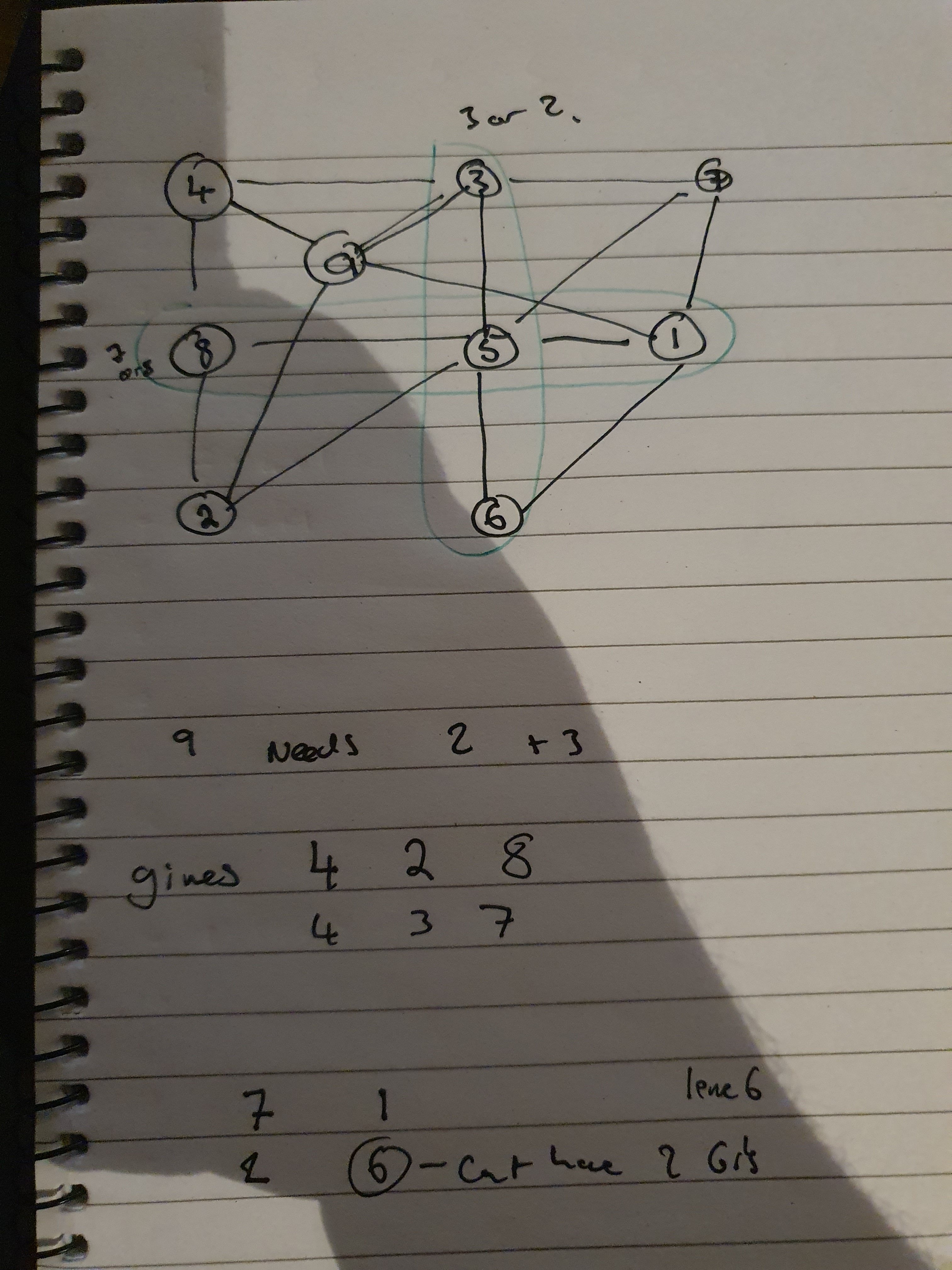
I enjoyed this puzzle, if you have any cool 1-9 puzzles do send them on.

A surprising fraction?

The other day I saw this tweet from John Rowe (@MrJohnRowe):

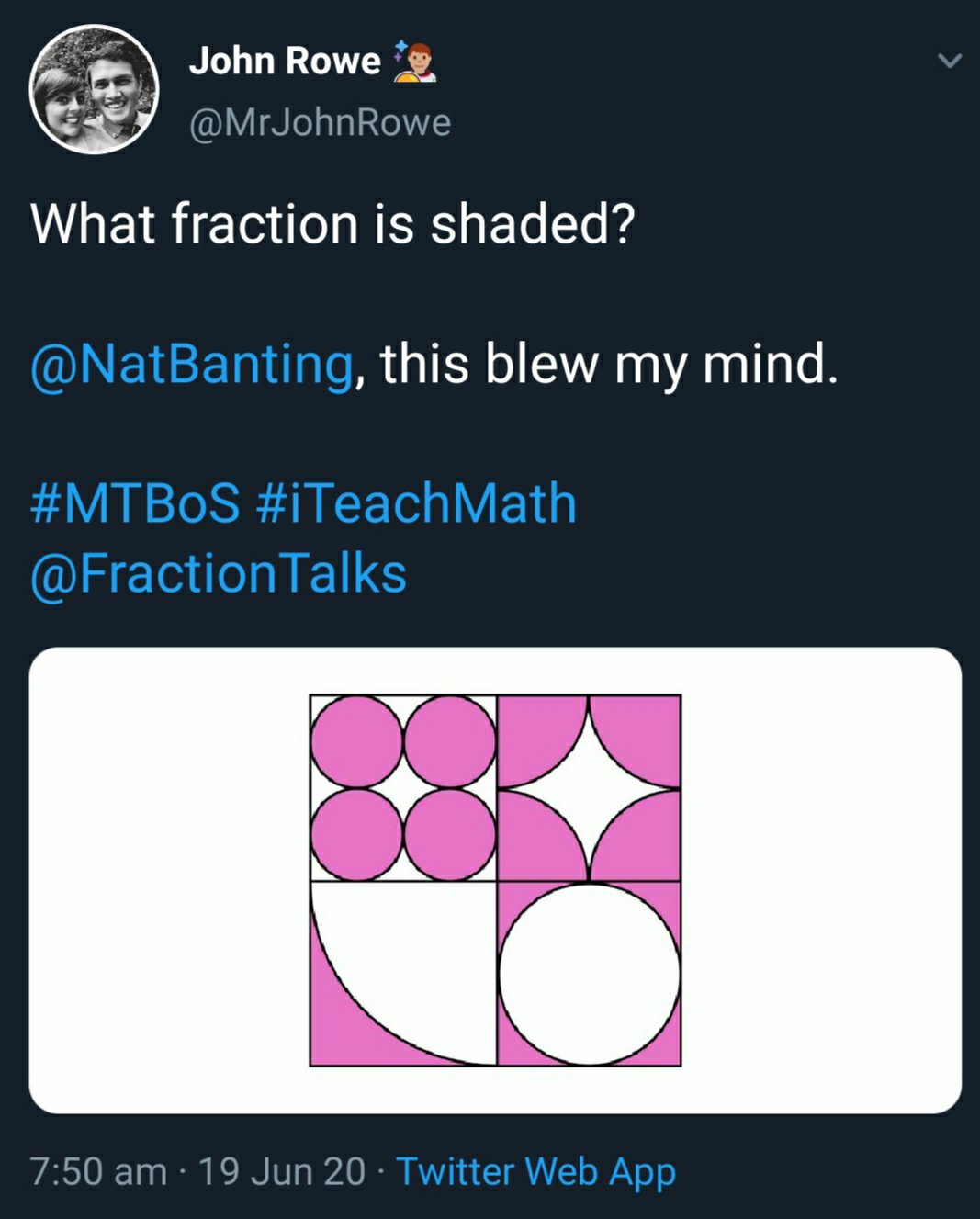
I looked at the picture and decided the answer was probably a half. And thought about it a bit more. The 4 small circles in the top left should be the same as the white quarter circle below, and the 4 quarter circles in the top right should fit over the white circle below them. This was interesting to me, and I thought I’d look at the algebra.

Looking at the top left corner, the circles involved there have the smallest radius, so we will call that radius r. That means each circle has a radius of pi r².

Below it we have a square the same size and a quarter circle radius 4r, so the white area is (16pi r²)/4 or 4pi r² this is the same as the pink area in the square above. We can see from this that half of the left rectangle is pink. Or we can continue with our algebra. The area of each square is 16r² (its sidelength is 4r) so the pink but here is 16r² – 4pi r², so if we add this to the bit above it we have 16r² shaded (and 16r² white).

The top right has 4 shaded quarter circles, each with radius 2r, so the total shaded area is 4pi r². Below it the white circle has the same radius so same area 4pi r², again that makes the shaded area 16r² – 4pi r² so the shaded area in the right rectangle 16r², and in the big square 32r². The total area of the big square if 64r² (radius is 8r) so the shaded fraction is a half. Which is nice.

Now I know I started by saying I thought it looked like a half, which is what I did think at the time I first saw it. But I still think it’s a surprise fraction. I’ve done a lot of geometry puzzles. And many have included shapes like this, so when I look at this that knowledge helps me see. Most students would not have done anywhere near the amount of puzzles I have so wont have that foresight, and I think it would be a very surprising result that could open many up to the wow factor. I also think that it might be a good starting point for some rich class discussions.

I think it’s a great visual and a lovely answer.