Pythagorean Triples

So, pythagorean triples. For those who don’t know, pythagorean triples are right angled triangles with integer (whole number) side lengths. The most famous pythagorean triple is the 3, 4, 5 triangle.

These triangles are great for maths teachers, as they can be used to make the arithmetic easier when introducing higher mathematical concepts. They are often favoured by exam boards for the same reason. Recently I have been working on the Edexcel M3 module and it seems that EVERY triangle they use is a 3,4,5 or a multiple there of. Noticing this fact has help my students and I save lots of time, we lost 20 minutes to this by not spotting it:

Yesterday we were revising FP1 and one of my students was finding the modulus of -7 + 24i, as she was typing the required sum into her calculator I said “25” to the general amazement of the class. They were intrigued as to how I did it so quickly, I explained I knew that the 7,24,25 triangle was a pythagorean triple and this led onto a fascinating discussion.

They thought it was an impressive trick, and I told them that yes, it was, and another good trick (courtesy of @icecolbeveridge) was knowing that the angles if a 3,4,5 triangle are roughly 53.13 and 36.87 degrees!

We discussed this further, and they asked how many triples I knew “off the top of my head”. I explained that I could write them forever if we weren’t limited to primitive triples, because I could just add 3,4 and 5 to the respective sides. This lead to a nice discussion about primitive triples. Which are those where the side lengths are co-prime (have no common factors). And then I wrote the primitive ones I could remember:

3,4,5
5,12,13
7,24,25
9,40,41

This prompted the question “is it some sort of sequence? I can see the smallest side is the sequence of odd numbers.” I was impressed how quickly they had spotted than, but I then remembered the 8,15,17 triangle which has an even numbered smallest side. I also told them that I have a vague recollection that there is  a way to use one primitive triple to generate another but I can’t remember it. (A quick Google search didn’t help, so perhaps I imagined it. If you know it, I’d love you to tell me!)

I then discussed Euclid’s formula for generating triples and then moved on to my favourite way:

Take two unit fractions with denominators one apart, add them. The answer in its simplest form will be a fraction in which the numerator and the denominator form the short legs of a pythagorean triple.

I’m not sure where I first heard this method, but I do love it and I often use it when working out questions to set my classes. I explained that this method shows there are infinitely many primitive triples, as it will generate infinitely many, but that I didn’t think it would generate them all. (Again, I don’t know if it will or not, I just imagine it won’t. Do send me a link to a proof either way if you have it!)

The class, interested and enthused as ever, wanted to see proof that this always worked. They had tried lots of numbers and they had all worked, but they knew this didn’t prove it. I then said we would prove it together.

I asked how we might start, had the word induction thrown at me, then one said,

“could we start with 1/m + 1/(m+2), then square the top and bottom of the answer and see if it’s a square?

I shouted “excellent” and so we did:

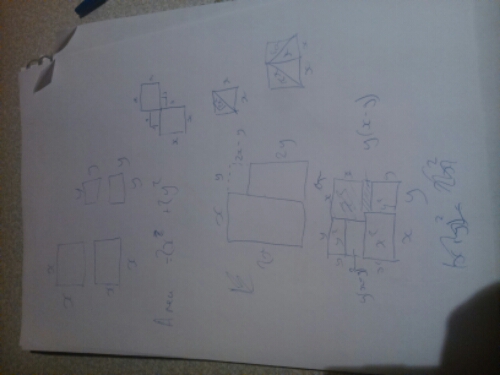
Obviously this isn’t the whiteboard… I forgot to photograph it so have recreated it on paper.

The start, adding the fractions:

Then squaring the numerator and denominator, manipulating the expression and factorising:

And finally, the all important statement:

Do you have a preferred method of generating triples? Or do you know any interesting facts about them? I’d love to hear them.

What does it mean?

Today my year 11s were busy revising ahead of tomorrow’s mock exam and one of them started singing the averages song. You know the one:

“Mean is average, mean is average, mode is most, mode is most, median’s the middle, median’s the middle, range high low, range high low.”

This got me thinking about the words we use. I’ve always disliked this song as a mnemonic as it encourages people to think of the mean as the “average” when actually the mode and the median are also averages too. The median in particular is a very useful one and we need pupils to understand the distinction. I have been very impressed in recent staff meetings to hear the principal, an English teacher by trade, use the term “national median” rather than “national average”!

As I was thinking about this, though, I had the sudden realisation that I should also be feeling the same way about the term “mean”! Granted, at GCSE level we only talk about one mean, the arithmetic mean, but that doesn’t mean the geometric mean doesn’t exist. (Nor the root mean square nor harmonic mean for that matter! Other means are available)

This is a hypocrisy in the way we treat certain words. I’m not the only maths teacher who dislikes the way mean and average have become synonymous. But no one has ever mentioned that the word arithmetic is missing from the term every time we use it.

I worry that we may be setting students who go on to further study statistics up for confusion in the future by simply referring to the arithmetic mean as the mean.

Have you ever used the term arithmetic mean, or even geometric mean, with your students? Have you shared my worry? Or do you think I’m being overly pedantic and it doesn’t matter? I’d love to hear your opinion.

Self fulfilling prophecies

I recently read the latest offering in Tom Sherrington’s (@headguruteacher) Pedagogy Postcard series.the series has been excellent and I would certainly advise any teachers or anyone else interested in teaching to have a read.

This recent post was entitled “Pitching it up“, and was discussing expectations. Tom was posing questions about how we see our classes and if we project limitations on to them. Do we, as teachers, miss things out of our teaching because we don’t think that a class will be able to cope with it?

This got me thinking deeper. Last week I was having a discussion with one of my year 11 students. He’s a bright lad and already has a number of GCSEs above the grade of C. But he tries to coast where possible and has a bit of a bad reputation amongst the teaching staff. We were talking about his plans for next year, he told me he had an interview at an FE college and he really hoped he got in because he wanted a fresh start. When I probed further he said he felt he needed one because “the teachers here know I haven’t been a hard worker, if I go there I can start again and they won’t have those preconceptions.”

This made me think a lot. Had I allowed him to get away with doing less than I would have allowed others to do because of preconceived ideas I had of him? Had my colleagues? How many preconceptions have affected the way I teacher people?

I thought long and hard about this, and I’m fairly sure that on the whole I don’t allow preconceptions to prejudice the way I treat my students. I have built great relationships with classes that I have heard colleagues write off as unteachable. I have been surprised to hear that some students are considered naughty when they are the stars in my class, and I’ve been surprised the other way too. Recently I was told be a colleague that the year ten boy I give tons of reward points to is in an almost permanent detention in numerous other subjects.

This must happen though, or the student in question wouldn’t have said that. It’s fairly understandable too. If you hear a name over and over again in a negative context then that name is going to have negative associations in your mind. We need to make an effort to fight against this, and to take the class in front of us as they are. Otherwise we run the risk of projecting negative behaviours onto them and creating self fulfilling prophecies.

Every student deserves a fair chance, and not to be tainted with a preconceived idea, whether that stems from staffroom hearsay, a troublesome older sibling or data received from a previous school.

Statistical Deception

When teaching and talking about statistics I always emphasise the need to be careful what you believe and to always ask yourself “what agenda does the person presenting this data have?”

I’ve written before about how stats can legitimately be manipulated to serve different points of views, especially when there are false variables at work. But recently I’ve noticed at darker art in statistical manipulation, one that is, at its heart, lying.

We are less than six weeks away from local elections now, and it is becoming silly season for party political leaflets coming through our letterboxes. Now we all know that the political parties will present data in a way that makes them look better, they are trying to win your vote afterall, but we would expect them not to lie. For the data to be accurate and presented correctly. Unfortunately, however, this is not always the case:

Exhibit A

This popped up a number of times in my twitter feed from a variety of sources. I believe it is from a Lib Dem leaflet in Manchester. As you can see, they have presented a bar chart with proportions labelled as percentages. The first screaming error is that the red bar and the orange bar are massively different heights, yet are both emblazoned by the label 39%. The second glaring error is that the percentages add up to more than 100%. The first implies that either the Lib Dems are deliberately trying to mislead voters into thinking they are in a stronger position in the ward than they are, or that they don’t realise that 39% is equal to 39%. I’m not sure which is worse?!

Here’s an excel interpretation of what the graphs should look like:

Exhibit B

This graph came through my door in Leeds North West parliamentary constituency. The first thing that caught my eye was that although the gap between the number of votes between Lib Dems and Labour; and between Labour and Conservative is almost the same, the difference in the gaps between the bars was almost 5 times as big, which would imply almost five times as many less votes! An obvious fallacy. Either it’s a deliberate attempt to mislead, or they can’t draw a bar chart. If it’s the latter, do we want them in charge of our local authority budgets?! (or the entire economy for that matter!!)

Something else that struck me as deciving, although this time mathematically correct at least, was the choice of data. This was a leaflet issued in the run up to a local election, and the data set used was from the last local election. Why then, is the data that for the parliamentary constituency rather than the council ward? The ward makes up around a quarter of the constituency, and the vote share in the ward is radically different to that of the constituency. The sitting councilor is conservative and sits on a huge majority, and the Lib Dem candidate last time out cane third. To issue a leaflet in the run up to a local election which implies the conservatives can’t win in a ward where they have a large majority and back it up with local election data for a parliamentary constituency is deliberately deceptive and misleading.

Here’s an excel interpretation of what this one should look like:

Exhibit C

This one comes from “across the pond” and is another which was viral. This one seemed to appear constantly for a few days everywhere I looked. If you are still wondering what’s wrong with it, take a little look at those numbers down the left hand side…. See it? The y axis goes upwards to zero! Drew Barker (@twentythree) made this version which gives a much better picture as to what’s going on.

I can’t wait to see what my classes make of these!

nb I haven’t “selected” these graphs as an attack on the Lib Dems, it’s just they are the only party who have sent me a leaflet with incorrect maths. I’ll gladly expose any of the parties if they themselves do. I do collect these, so if you spot anything similar, do send me it!

An Acute Problem

Prove that for an acute angled triangle ABC sinA + sin B + sin C > 2.

This is a problem that was posed to me at a meeting of the Further Maths Support Programme (@furthermaths) in Leeds a few months ago that stumped me for quite a while, but once I realised how to the answer it seemed fairly obvious.

I believe the question originally came from a step paper (ie Oxbridge entrance exam) so it is aimed at an able A Level student.

Without meaning to patronise, I want to clarify the wording incase anyone was unclear. An acute angled triangle is a triangle where all the angles are acute. The vertices are labelled A, B and C. The problem is looking for a proof that the sum of the sines of the angles is always greater than 2.

When I first encountered the problem I set off on all sorts of dead ends. Dropping perpendiculars, equating this, equating that, all to know avail. Then I drew the sine curve. At first I was just staring blankly at it, then I considered just the portion of the curve which relates to acute angles. Then I saw this:

A straight line from the origin to pi/2 (or 90… I don’t know why I did it in degrees on this picture!) would prove that for all acute angles sin x > Pi/2 (or sin x > 90 in degrees).

From there it was pretty straightforward:

So there you have it, for any acute angle, x, it’s sine, sin x, is greater than x/90. (I’m just going to work in degrees now, as that’s what’s on the photo!).

So:

Sin A > A/90

Sin B > B/90

Sin C > C/90

Hence:

Sin A + Sin B + Sin C > A/90 + B/90 + C /90

> (A+B+C)/90

> 180/90 (as A B C are the angles on a triangle)

>2

A lovely simple solution when you see it! But hard to find at first.

And in radians:

A sphere and a frustum

A sphere and a conical frustum have the same volume, the frustum has a base radius which is twice the radius of its top. The sphere has a radius which is equal to the base radius of the frustrum. What is the ratio of the diameter of sphere to the height of the frustum?

Recently the podcast “Wrong, but Useful“, (@wrongbutuseful) celebrated its 1 year anniversary. The hosts Dave (@reflectivemaths) and Colin (@icecolbeveridge) asked listeners to send in messages to be played on the anniversary show.

I thoroughly enjoy the podcast, and particularly the part where the hosts set puzzles for the listeners to have a go at. With that in mind, I decided to set a puzzle for them as part of my messages.

I know a number of puzzles, but I didn’t want this to be a problem either of them had heard before, so I set about devising one. I thought about the problems I like to discuss, and remembered that I’ve always liked the algebra based geometry problems that occur at the back of GCSE papers, you know the ones: “Three tennis balls radius r fill a cylinder… What’s proportion of the cylinder is empty space?” etc.

I thought a problem like this would be nice. I thought about it and decided I wanted to use a sphere and a frustum with the same volume. I decided that the frustums base radius should be twice the radius if the top and that I would ask them to find the ratio of diameter of the sphere to height of the frustum. I needed to think about the radius of the sphere. At first I thought it might be nice to have the sphere have the same radius as the top face of the frustum, but I reckoned that wouldn’t give a very satisfying answer as it would have hardly any height to speak of. So I tested (on a magna doodle no less) to see what it would be if I used the base radius as the same as the sphere:

Volume of a sphere: (4(pi)(r^3))/3

Volume of a frustum: ((pi)(h)(r^2 + rR + R^2))/3

Sub r=r, R=r/2

Equate equations

Cancel pi/3 from each side

4r^3 = (7/8)(h)(r^2)

16r = 7h

8d = 7h

Ratio d:r is 7:8

What a nice, simple, solution we get from quite a bit if algebra. I thought that as it fell out so nicely I would set it!

I realised that for Dave, Colin their listeners and the majority of people I posed this question to would not really have had too much of a problem solving it, but hopefully will have enjoyed it. I did think, however, that it would be an interesting problem to pose my yr11s (and my sixth formers). They have all the skills and knowledge required, so it will be interesting to see how they get on. I will pose it to them after the holidays!

Resilience in the classroom

Recently I’ve written a lot of posts around puzzles and problems that people have set me to solve. This is something I find fun to do and I have enjoyed solving them. I have also enjoyed sharing my thought processes and proofs here, including the dead ends I went down.

The ideas involved in doing this have led me to think a lot about which, if any, of my students would have been able to solve each of the problems.

I started thinking about my A level classed, I know that the vast majority would have given them a go. One or two might have not started because they didn’t know where to start, but the rest would have given it a try. I’m fairly certain that at least 5 of them, given enough time, would have solved most of the puzzles. I intend to test this hypothesis after the holidays.

I then thought about my year 11 class. They are a top set and I have been trying to build a resilience in them this year. When I first took the class over in September one of the students complained to my colleague, her science teacher, that I had “given a worksheet and not even told us how to do it.” It had been a starter task designed to double check the class were familiar with and able to use Pythagoras’s Theorem. My colleague then asked her “could you not do it then?” to which she had replied “I could actually, it was Pythagoras’s Theorem.” He then asked, “so why did you want him to tell you what to do?” She had no answer.

This is quite common in schools, it’s an idea a lot of pupils have. That they should be explictly told what to do for each type if question. But I think that if we are to create the mathematicians of the future we need to be building a resilience into pupils. We need to equip them with the skills and knowledge required to solve the problems, and allow them to select whichever bit of it they want/need to solve it.

I think the puzzles I’ve discussed recently are good examples of tasks that do this. Some of them have the added bonus of being solvable multiple ways, often given rise to a “low barrier, high ceiling” task that can be set to 11-18 year olds and be solvable, yet challenging, to all.

This one which started the chain is a lovely puzzle based around algebraic fractions. It is solvable to a clever yr7 student who just has a basic knowledge of fractions, or via simultaneous equations and complex numbers, which is how most people with an advanced knowledge went about it.

This triangle puzzle was particularly nice, it had a lovely solution which requires a knowledge of the sine rule for the area of a triangle and knowledge of the sine curve, or a much simpler visual one which only requires a primary school level understanding of triangles!

This triangle puzzle is the best example of one with multiple solutions. I used Heron’s Formula (which no one else seems to have heard of!) But it is equally solvable using accurate drawing, similar and congruent triangles rules and/or Trigonometry (including Pythagoras’s Theorem).

These problems are great, and will build resilience, but the two most recent ones are the ones which illustrate this best.

While discussing constructing a proof with my brother he was asking how algebraic proof worked. He has two A levels in maths (at A no less) but he stopped studying maths a decade ago so is a little rusty. His questions, though, made me think about my classes. I know my year 13 pupils can construct proofs, but I’m not sure about all of those pupils who are younger. I am going to ensure I build more opportunities for this into my lessons.

In solving this problem I noticed a pattern in the numbers, I expressed this pattern algebraically and manipulated the algebra to prove the pattern was true for all numbers. This is what mathematicians have done for centuries and how theorems are born. And this is a skill I need to instil in my students.

In the root of the problem I discussed solving a problem which involved searching for integer solutions of an equation in two variables. It was fun, and again I was asked, “how on earth did you work that out? I wouldn’t know where to start.” Well I didn’t know where to start either, I just tried things until I got something that was right. This is what the best of my students do. This post gives some great examples of this. It needs to be more though. As maths teachers we need to make sure our students are willing to do this, if they don’t know what to do to apply things they know until they get an answer. I have been using this approach with my pupils. I won’t help them unless they have tried something first.

The way the maths exams have been previously has made this spoonfeeding possible and far too common. In the last couple if years the exam boards have thrown a few curveballs, which has meant that students have had to apply their knowledge in different ways to the past papers. I think this is the way forward, and hope the new GCSE and A Level exams address this.

The root of the problem

Yesterday, while discussing various proofs and problems, my friend Steve posted this and said it was his favourite problem of the last few years.

He laid it down as a challenge for me and the others involved in the discussion to solve.

The question:

Find all solutions in non negative integers a,b to (a)^1/2 + (b)^1/2 = (2009)^1/2

I was out when I saw the question so couldn’t crack on with it straight away, but I did throw a few ideas around in my head. My first thought was “one equation, two unknowns, Hmmmm, I could square it, rearrange the original and sub it it to eliminate, actually no. I would just be proving a=a, b=b, and 2009=2009 then, so that’s a bit silly.” It always amuses me when I, or someone else, manages to prove something like this. My Year 13s still laugh about the time one of them started and finished with F = ma after two pages of working!

My next thought was to complete a prime factorisation on 2009. As it happens I didn’t need to my brother posted “I’ve simplified root 2009 to 7root41” which was what my prime factorisation was for. I realise now that I probably should have seen the answer and this point, but I didn’t.

I thought it would be a good idea to rearrange the equation to find a:

I replaced root 2009 with 7 root 41 and then it was clear: for a to be an integer, b has to be a multiple of 41. This is because any integer b would make the first and last terms integers, but only multiples of 41 will make the middle term an integer. The term is 14x(b)^1/2(41)^1/2 and you need a root 41 to rationalise the one that’s there. Moreover, b must be 41 multiplied by a square number, as any other factors of b would leave another surd.

From there it was easy to spot the answers.

The root a term plus the root b term must equal 7 root 41, so if root a = root 41 then root b = 6 root 41. Likewise if root a = 2 root 41 then root b = 5 root 41. In general if root a = n root 41 then root b = (7-n) root 41 (n is a natural number less than 7). Eliminate your roots and you get {a,b} = {41n^2, 41(7-n)^2} n € N, n < 7.

A truly lovely problem, with a thoroughly beautiful solution.

Nb I apologise for my inability to code the correct maths symbols etc.

Constructing a proof

Yesterday, while discussing this problem, my friend Steve posed this problem that he’d been thinking about:

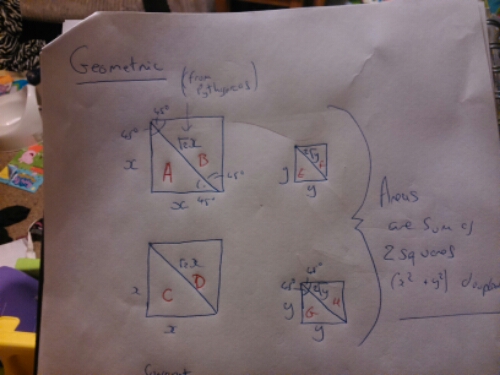
The sum of two squares doubled is the sum  of two squares. Prove it algebraically and geometrically.

Being the sort of person that can’t let a puzzle go unsolved I picked up a pen and set to work. I started with 2(x^2+y^2) and thought about where to go next. As I was doing this my brother (@andycav_25) posted

“1 seems to be always involved as one of the squares in the doubled bit”

then

“With 5 and 6 you get 122. 11^2 +1

2 and 3 give 26. 5^2+1

So it’s the sum of the first 2 squared plus 1″

I could see his error straight away, he had only tried consecutive numbers, I tried 2 and 6. 4+36 = 40 doubled is 80. 2+6=8 and 8^2 is 64. 80-64=16. And there you have it. It’s not the sum of the numbers squared add one, it’s the sum of the numbers squared add their difference squared. All I had to do now was construct a rigorous algebraic proof that would work for all numbers:

Nice isn’t it. The two squares are x^2 and y^2, their sum is (x+y) their difference is (x-y). Set up your equations, show they are equal and there you are, a proof that works for whatever numbers you like. The one case where it doesn’t fully work is where x=y. This relies on the second square being zero. However, the question relies on the same thing, as 2^2 + 2^2 doubled is 16, which is the sum of 4^2 + 0^2 but not any ‘other’ two squares. If 0^2 doesn’t count then this counter example disproves the statement. Perhaps the question should read:

Prove that the sum of two squares doubled is either a square, or the sum of two squares

That works better, and is how I’m going to pose it!

I like algebraic proofs, I’m comfortable with them, I’ve worked with them alot, I know how to do them and have been known to do them for fun. This is a good example of how they come about, you noticed a pattern, like Andy did, test some other numbers, like I did, hypothesise the general case and try to use algebra to prove it.

Geometric proofs, however, are a trickier beast. I didn’t opt for many geometry based courses at uni and I’m not as experienced at constructing the proofs. I’m never fully sure what constituents a geometric proof. Is a visualisation of an algebraic proof good enough, or is that just an algebraic proof expressed a different way?

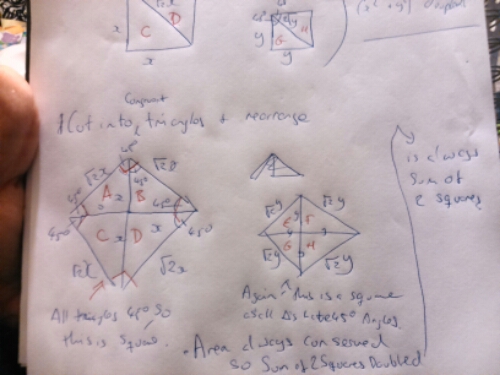
I don’t shirk a challenge, however, so I wanted to have a go. It was even harder than I thought. Here are some early attempts:

Then I had thought I had had break through of sorts:

I thought I had cracked it, but now I’m not sure. I’ve lost a bit of confidence in it. Does it proof what it is supposed to? Area is definitely conserved. The total area of the top is definitely the sum of two squares doubled:

and the bottom is clearly two squares.

It works whatever size the squares are. However the implication in the question is that we are looking for integer side lengths, so I’m fairly sure it isn’t correct. Back to the drawing board!

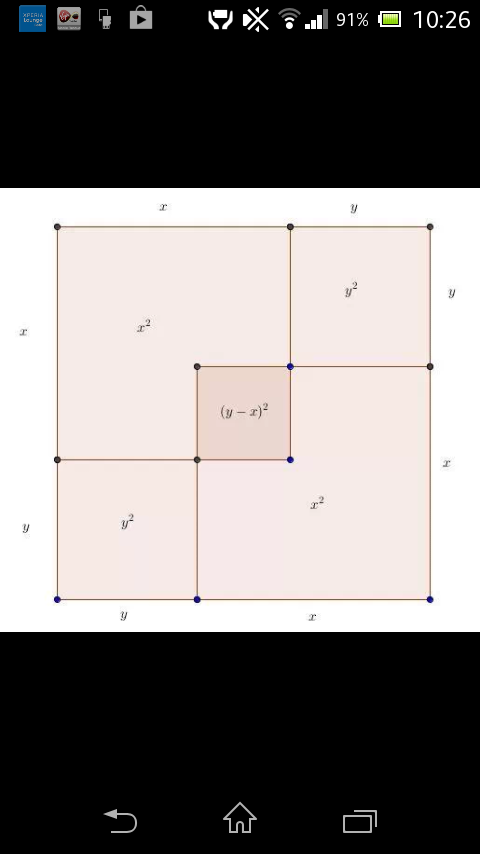
Steve, who originally brought the puzzle to my attention, constructed this lovely visual proof:

We have 2x^2’s and 2y^2’s which make an (x+y)^2, and with an extra (the overlap) (x-y)^2 therefore 2(x^2 +y^2) = (x+y)^2 + (x-y)^2.

It’s definitely a proof, and a lovely neat one at that. Does it count as a geometric proof, or is it just a visual proof?

I’d love to hear your opinions. I’d also live clarification on what a geometric proof is. Do tell me if you can come up with a geometric proof that works.

Area the Hero’s Way

This morning I posted this about a lovley simple triangle puzzle I had found and explored. One of the responses came from Mrs Watson (@MrsJMWatson) who tweeted this reply:

The link is to this page from Nrich and contains this puzzle:

Triangle T has sides 6,5,5 and Triangle Q has sides 8,5,5 What is the ratio Area T:Area Q?

Now this is a great example if a “low barrier, high ceiling” problem. I think your first instinct are probably to go with what you are most familiar with. In today’s earlier problem the respondents who are used to working with the sine rule for area instinctively went for that, but others who are more used to working with other things went other ways.

For this problem my instinct was to use the cosine rule to find an angle, and then the sine rule for area ((1/2) absin(c)) to find the areas and simplify the ratios. My friend Steve, also a math teacher up to A level, actually worked through this, but didn’t need the sine rule for area as the ratio is easy to spot when you see the angles add up to 180 degrees (we’ll let him off for using degrees just this once).

I didn’t go down this route, I was thinking about generalising for all triangles and thought Heron’s Formula would be better for this.

I used it and found this lovely solution:

T) a=5,b=5,c=6 s=8
Area: (8.3.3.2)^1/2=12 U) a=5,b=5,c=8 s=9
Area:(9.4.4.1)^1/2 = 12

So Area T: Area U = 12:12 = 1:1

Discussing my method and answer with various people today I have been shocked at how many people (most it seems) haven’t heard of “Heron’s Formula”!

Heron’s Formula

Heron’s Formula is a fantastic piece of mathematics. I don’t know how I know about it. I have known about it so long it didn’t occur to me others wouldn’t. I guess I had assumed I learnt it at school, but if that was the case others would know about it. I’ve read and watched a lot about maths over the years, so I guess I must have picked it up from a book or show.

For those of you who don’t know, Heron’s Formula states:

For a triangle with side lengths a,b and c

Area=(s(s-a)(s-b)(s-c))^1/2

where s is the semiperimeter (ie s=(a+b+c)/2)

A truly marvellous formula. It’s named after Hero of Alexandria, who along with this formula is credited with being the first person to envisage imaginary and complex numbers.

Hero’s own proof is pretty cool, and involves cyclic quadrilaterals and properties of right angles triangles. There are lots of other proofs too, my favourite is the trigonometric proof, which I think would have been what I ended up with if I had decided to generalise this problem using trig!

Later in the discussion Mrs Watson said the phrase “Pythagorean Triples“, and I instantly saw both triangles could be cut into 2 3,4,5 triangles. I think this is the nicest solution. When I checked back to another discussion I noticed that Andy (@andycav_25) had also had this realisation. His instinct was to draw a perpendicular height. I wondered if I would have gone down this route if I’d had paper to work on instead if working mentally?!

Finally, Mrs Watson mentioned that her year 7 class do it via construction. She didn’t elaborate much on this, but I imagine she means draw both triangles accurately, measure the height, work out the areas. This is, in itself, quite nice, and shows that pupils can tackle the problem using whatever tools they have at their disposal.

This is a lovely problem, I’d love to hear how your instincts would tackle it, how your students for if you try it, and if you previously knew about Heron’s Formula!